Quantum Error Correction, an informal introduction. Start. <-- [prev] .

---

6. Dual codes and correction of general errors

To recap, so far we have learned about parity check measurements and the use of the repetition code 000,111 for bit-flip correction. We then discussed its use for phase-flip correction using the second basis, and we showed how this also permits the correction of "collapse" or "projection" errors.

We introduced in section 4 an insight which will turn out to be highly important, namely that

|000...0> + |111...1>	=	Σj	(1 + (-1)j) |j ">
	=		|even ">

That is, the equal superposition of all-zeros and all-ones gives, in the other basis, the equal superposition of all bit-strings of even parity. In classical coding terminology, the equal superposition of all members of the n-bit repetition code in the first basis is the same as an equal superposition of all members of the n-bit even parity code in the other basis.

Now, the repetition code and the even-parity code are close cousins in classical coding theory. They are a pair of what are called dual codes. For a dual pair, all the members of one code satisfy all parity checks represented by members of the other code. In the example just given, the repetition code offers the trivial parity check "000...0" (meaning don't examine any bits) and just one other check, the overall check "111...1" (meaning, obtain the parity of the complete set of bits). The even parity code satisfies both these checks. Equally, the even parity code members, when interpreted as parity check strings, offer check strings such as 000...0011 and 000...0101 etc.. The repetition code satisfies all these.

6.1 Some more classical coding theory

Let's play with this idea a little further. The repetition code is only the most simple of a vast array of classical codes. Further codes can be constructed by insisting that the bit-strings satisfy either more parity checks (in the case of the even weight code) or fewer parity checks (in the case of the repetition code). For use in error correction, a desirable property is that the members of a code should be at high distance from one another (measured by how many bit-flips are required to convert one codeword into another). Recalling the idea that binary bit-strings can be regarded as vectors in an n-dimensional lattice, we see that errors move a codeword away from its initial point in the vector space. As long as all other legal codewords are a long way away, it remains possible to identify the codeword correctly from its corrupted version. Each codeword has a "zone of correctability" around it (see figure). For this reason a crucial property of the code is its minimum distance, defined as the shortest distance between any pair of bit-strings in the code. You should be able to see that a code of minimum distance d allows correction of all corruptions involving less than d/2 bit-flips. It is said to be a "t-error correcting code" with t=(d-1)/2 (for odd d), or t=(d/2-1) (for even d).

The discovery of good sets of checks, i.e. ones that constrain the code to have high minimum distance, is a rich subject. The diagram at the left shows all the members of the 32-bit "Reed-Muller" code (to bring out the pattern, the diagram shows a white square for zero, black square for one). This code was used by the Mariner space probe in 1969 to send back images from the planet Mars. There are 2⁶=64 codewords, and they all differ from each other in at least 16 places, so the minimum distance is d=16. Therefore this is a 7-error-correcting code. With 2⁶ words to choose from, 6 bits of information can be encoded, so we say k=6 bits are encoded into n=32 bits. The ratio k/n=0.1875 is called the rate of the code. This is a powerful code: if the noise is random and at a level below a few percent error probability per bit, then the correction is essentially perfect. No wonder the Mariner pictures look so clear!

For a classical linear code in n bits, the number of codewords is always a power of 2. If the number of linearly independent parity checks is m then the number of codewords is 2^k, where k = n - m. Hamming introduced a general construction for single-error correcting codes which is easy to understand. Consider the following parity check matrix:

1010101

0110011

0001111

Each row of the matrix is one parity check which all the codewords must satisfy. Since m=3 and n=7, this code has k=4, i.e. 16 codewords. Notice that the columns of the matrix are simply the binary numbers from 1 to 7. Suppose we start with a codeword (for example 0000000), then all 3 checks are satisfied. Now suppose an error flips one bit. We would like to know, can a measurement of the checks tell us which bit was flipped? The answer is yes, because the outcomes (even/odd) of the three checks exactly indicate the binary number identifying the bit-position of the flipped bit! (Try it and see).

Clearly, this construction can be extended to any number of bits, as long as we include enough rows in the check matrix so that the parity check results can "count up to n", i.e. 2^m > n.

For other code constructions, the reader should consult a standard text on coding theory. For present purposes, the main thing we need is a reminder on the idea of a dual pair of codes. If a code has codewords {u_i}, i=0...(2^k-1) which satisfy parity checks {p_j}, j=0...(2^m-1) then the codewords of the dual code are {p_j}, j=0...(2^m-1) and they satisfy parity checks {u_i}, i=0...(2^k-1). Recalling that k + m = n, it is clear that when a code has 2^k members, its dual has 2^n-k members.

6.2 Back to quantum

Now we return to our study of quantum coding.

In the spirit of enquiry, let's simply write down an equal superposition of the members of some code, in the 0,1 basis, and see what we get in the 0",1" basis. The next most simple code, after a 3-bit repetition code, is perhaps 0000,0011,1100,1111. That doesn't teach us much, however, because it can be understood as a 2-bit repetition code used twice. Therefore let's go on to 5 bits, where we have for example 00000,00111,11100,11011. We now have 4 bit-strings (classical codewords), and they all differ from one another in at least three places (I carefully chose them to make sure of this). Also, they form a linear code, meaning, when you consider the codewords as vectors, and add together any pair, the result is still in the code. These codewords satisfy three linearly independent parity checks, such as 00011, 11000, 10101, and it follows that they also satisfy all linear combinations of these checks, i.e. {00000, 00011, 11000, 11011, 10101, 10110, 01101, 01110}. Now we write down the equal superposition of the codewords in the first basis, and examine what we've got in the second basis. The answer is:

|00000> +|00111> +|11100> +|11011> =
|00000"> +|00011"> +|11000"> +|11011"> +|10101"> +|10110"> +|01101"> +|01110">

We observe that what we earlier noticed for the repetition and even parity codes still holds true, and this is a crucial result: a given linear code in one basis (expressed in equal superposition) produces the dual code in the other basis! It is not hard to prove this.

For quantum error correction what we want is a dual pair of codes, both of which allow classical error correction (that is, both having minimum distance ≥ 3). This will lead to the possibility of both bit-flip and phase-flip correction together. At this point in the argument, a version of the Heisenberg uncertainty principle comes into play. Let M be the number of words in a code. For any dual pair of classical codes C₁, C₂, we have the property

M₁M₂ = 2ⁿ.

Now, to allow correction of errors, we need to have few codewords (so that they can be far apart). However, the above relation shows that if one code has few codewords (to allow high distance), its dual has many, and therefore can't simultaneously have high distance. The best we can do is to accept a compromise, and choose pairs with similar size and similar minimum distance, M₁ ≈ M₂ ≈ 2^n/2, and d₁ ≈ d₂ .

The final step is to see how we can marshall all these resources to make a quantum code. A 'quantum codeword' must be a quantum state which allows correction in both bases at once. Therefore it can't consist of a single codeword from a classical code. Instead, a quantum codeword can be composed of all the members of a classical code, in equal superposition. This ensures that correction in both bases (and thus correction of both bit-flip and phase-flip errors) will be possible (as long as the code and its dual both have minimum distance 3 or more). Furthermore, to allow a qubit of information to be encoded, we need a second quantum codeword, and we need it constructed so that superpositions of the two codewords can also be corrected. This means they must both satisfy some set of parity checks. The trick is to see that if the superposition

|first quantum codeword> + |second quantum codeword>

is to be correctable, then we might pick the two codewords to be made from two subsets of a classical code. Perhaps the simplest way to understand this is to see an example. The smallest example is built using the 7-bit Hamming code introduced in section 6.1 above. The complete classical code is

0000000,	1010101,	0110011,	1100110,	0001111,	1011010,	0111100,	1101001
1111111,	0101010,	1001100,	0011001,	1110000,	0100101,	1000011,	0010110

As our first quantum codeword, use the first half of the code:

|0>_L = |0000000> + |1010101> + |0110011> + |1100110> + |0001111> + |1011010> + |0111100> + |1101001>

and the second quantum codeword is formed from the second half of the code:

|1>_L = |1111111> + |0101010> + |1001100> + |0011001> + |1110000> + |0100101> + |1000011> + |0010110> .

The subscript L is for "logical". We say these are the two legal states of the "logical qubit" encoded using 7 "physical qubits".

Both these codewords satisfy the parity checks

1010101

0110011

0001111

and these checks are sufficient to identify any single bit-flip error. The first quantum codeword satisfies the further parity check 1110000; the second quantum codeword precisely fails this check (i.e. all contributions agree on odd parity for the first 3 bits). This means the first quantum codeword is itself a code. Upon examining it in the conjugate basis, we find the equal superposition of all members of the dual, and that means the superposition of its 2⁴ parity checks. But these give precisely the very Hamming code we started with! This is because the Hamming code has the property that it contains its own dual as a subset. It follows that phase-flip correction is possible for the first quantum codeword. It remains to show that phase-flip correction is also possible for the second quantum codeword, and for arbitrary superpositions of the two. It is, because the second quantum codeword is obtained by flipping the first 3 bits of the first quantum codeword; these bit flips appear merely as sign changes (phase flips) in the conjugate basis, therefore whatever combination of the two quantum codewords is formed, the expression in the conjugate basis only ever contains members of the dual code, and is therefore correctable.

I promised that this would be a "friendly" introduction, but the reader may feel it has become rather abstract. Therefore I want now to offer some pictorial ways of seeing the main points.

Recall that classical bit strings can be regarded as vectors on a square lattice (in high dimensions). It follows that a classical code is a set of points on such a lattice. I picture it in my mind as somewhat like a crystal (see figure). In the classical case, each point in this crystal is one codeword. In the quantum case, the crystal as a whole is a single quantum codeword. Bit-flip errors move the crystal as a whole around the space. Further quantum codewords consist of displaced versions of the same crystal, separated from each other by as much as possible.

I think of the dual operation (i.e. converting a code to its dual) as something like "turning the crystal inside out". I'm only using this phrase in a very vague way, but it conveys the idea that the dual is directly related to the code, and I keep in mind the property that a small code (few vertices) has a large dual (many vertices) and vice-versa. Phase-flips displace the dual as a whole.

To actually carry out the quantum error correction, we need to measure the parity checks first in the usual basis (to obtain the syndrome for bit-flip errors) and then in the conjugate basis (to obtain the syndrome for phase-flip errors). This can be done, for example by the following network:

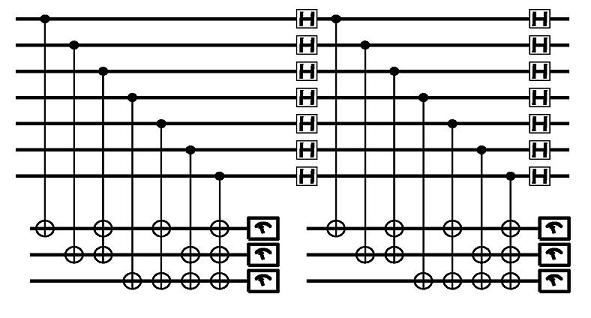
The H symbols are "Hadamard" gates that rotate between the two bases 0,1 and 0",1". The detailed proof that this all works as advertised is contained in the early papers, and subsequent textbooks or tutorials, where it is usually presented in a more succinct mathematical style. I will give some pointers on the more general mathematical tools and code constructions in the next chapter. Let us conclude this chapter with one further way to describe the quantum error correction process.

6.3 Quantum space

A quantum system such as a set of qubits exists in our ordinary 3-dimensional universe. The same can be said of a set of classical bits such as mechanical switches, or magnetic domains, or capacitors. However, the mathematical description of the state of a set of qubits, which captures all the subtleties of their joint behaviour, can be regarded as describing an abstract mathematical "arrow" in a high-dimensional space. This is similar to the vector space which we introduced as a useful way to picture the behaviour of classical bit strings. In the quantum case, the space is continuous not discrete, and the vector in the space is described by complex and not just real numbers. This "complex vector space" is called Hilbert space after the mathematician David Hilbert who studied it. The mere name Hilbert space can be daunting to students, but we don't need to let it worry us. Just think of the quantum state as a single arrow in a high-dimensional space.

Errors cause this arrow to move around. A bit-flip will rotate the arrow by 90 degrees about some axis, a smaller error will rotate it by a smaller amount. The measurement process in quantum mechanics disturbs the arrow in a very specific way: it projects it. If we imagine an arrow in three dimensions as casting a shadow onto a plane, then a projection would cause the arrow to move down onto the plane until it was superimposed on its shadow. The plane is a smaller (because 2-dimensional) "space" in which the arrow now exists. For multiple qubits, the dimension of the space is much larger (2⁷ = 128 dimensions for 7 qubits) but the general idea is the same. In a quantum error correction, the parity check measurements project the system multiple times (6 times for the 7-qubit code), forcing it to "decide" (randomly) which subspace to adopt. The "discretizes" the errors: a small error is either projected by good fortune back to no error, or it is amplified to a rotation by 90 degrees (i.e. bit-flip or phase-flip or both). Meanwhile, the measurement outcomes are available to help us know which flips occured if they did, so that they can be reversed afterwards. The whole process fails when the errors conspire together to rotate one legal logical state towards another legal logical state, but this requires correlated behaviour among multiple qubits, which is highly unlikely when they are undergoing independent random noise.

If the qubits are themselves undergoing correlated noise, then, just as in classical error correction, the code must be designed accordingly. In general, the main features of any noise process can be protected against.

[prev] <-- .