Quantum Error Correction, an informal introduction. Start. <-- [prev] . [next] --> |
5. Correction of phase errors
A "phase error" was defined at the end of the previous section. It involves a rotation of a qubit by an angle φ , without a bit flip. Now, to keep things simple, we are going to consider in the first instance just the value φ = π . The error process is then
(a |0> + b |1> ) ↔ (a |0> - b |1> ),
which may be called a "phase flip". Putting a = b = 1 into this formula, one sees that a phase flip is the process |0> + |1> ↔ |0> - |1> , which, recalling the definitions from section 3, is
|0"> ↔ |1">.
This simple observation is crucial: a phase flip in one basis looks like a bit flip in the other basis. It is crucial because it immediately shows us how to correct phase flip errors: we need an error correcting code in the new basis! For experts in quantum mechanics, this point is very easy to take in, but in these pages I am trying to be friendly, so I will elaborate on it a bit further.
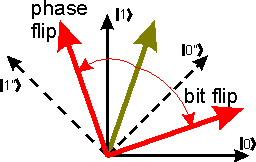In the diagram on the left, the black arrows represent the standard
basis vectors
{|0>, |1>} and the dashed
black arrows the second basis vectors
{|0">, |1">}. The green
arrow shows some general vector. The effect of a bit-flip error is shown
by the red arrow marked "bit flip" (it is a reflection in the diagonal line).
The effect of a phase-flip error is shown by the red arrow marked "phase flip"
(it is a reflection in the vertical line). The diagram illustrates that these
two types of errors are doing similar but complementary
things to the quantum state. A full mathematical analysis includes the fact
that the coefficients of the vectors can be complex, not just real numbers,
which can't be easily shown on this type of diagram. The full analysis
also makes clear that these error processes are rotations not reflections. The
main point is that the quantum state can be expressed either as a combination of
|0> and |1>}, or as
a combination of |0">
and |1">, and it will be useful to switch between
both points of view, depending on what error process is under consideration.
The reader can now guess, correctly, that a good quantum error correcting code for phase flip errors is the pair of "quantum codewords" |000"> and |111">. To correct phase errors one needs to measure parity checks in the {|0">, |1">} basis and the argument proceeds as before.
Do we now have a way to correct both bit flip and phase flip errors together? The answer is no, not yet. One way to see why is to take our bit-flip error correcting code |000>, |111>, and see what happens when a phase-flip occurs: the state |000> is unchanged while the state |111> changes sign. Suppose the message state being sent is |000> + |111>, for example, and a phase flip occurs. The difficulty is that the person or machine receiving |000> - |111> has no way of telling that this was not the message actually sent.
It is instructive to take a look at the situation just described using the other basis. The state |000>, when expressed in the {|0">, |1">} basis, gives a superposition of ALL possible bit-strings. This rules out the chance to introduce parity check measurements in the second basis. Therefore we don't have a way to detect phase flips in this case. We have to choose between either bit-correction (using |000>) or phase-correction (using |000">).
5.1 Projection and measurement-like error processes
Before we proceed to general quantum error correction, there is a rather beautiful further result of phase-flip error correction to mention. We have already alluded to the fact that in quantum physics the process of measurement is a physical process which can't be made negligibly small. That is, it must unavoidably disturb the system being measured (except in special cases). If we send qubits down a channel, and while in transit the qubits are examined in detail, that is, measured, by some person or process, then they will in general suffer large changes of state. This is a type of noise process, in which the changes amount to a "collapse" of the state, that is, a large and intrinsically random change. It seems remarkable that we can "resurrect" a state after it has suffered this type of collapse, but it turns out that we can. For quantum experts this is easy to prove mathematically, by using the fact that the collapse is described by a projection operator, which can be expressed as a combination of the identity and a phase-rotation operator. Therefore measurement-induced collapses are just like phase errors and can be corrected accordingly. It is instructive to examine an example to see how this works out in practice. Let's choose the phase-flip error correcting code {|000">, |111">,}, so a general "encoded" qubit state is
|y> = a |000"> + b |111">.
Recalling what we have been learning about states such as |000"> ± |111">, we rewrite this as
|y> =
(a + b)
(|000"> + |111">)
+
(a - b)
(|000"> - |111">)
=
(a + b)
(|000> + |011>
+|101> + |110>)
+
(a - b)
(|001> + |010>
+|100> + |111>)
(dropping normalization constants). Now pick any qubit, and suppose it is measured in the standard basis. To have a specific example, we'll pick the first qubit. Then, by looking at the second line above, where the state is shown in the {|0>,|1>} basis, we see the measurement forces the state to change to
| either | (a + b) (|000> + |011>) + (a - b) (|001> + |010>) | (all cases with a 0 in the first qubit) |
| or | (a + b) (|101> + |110>) + (a - b) (|100> + |111>) | (all cases with a 1 in the first qubit) |
The idea is that the measurement is a noise process, so we won't know which outcome happens. However, we now measure the parity checks in the {|0">, |1">} basis, so let's see what the state looks like in that basis. It is
| either | (a |000"> + b |111">) + (a |100"> + b |011">) |
| or | (a |000"> + b |111">) - (a |100"> + b |011">) |
In each case, the state is a superposition of the error-free original state and a version of it with a single flip. This is the situation after the "collapse" induced by the noise process, and before we have done anything to correct it.
Now we implement the parity check measurements. They force the system to adopt a state of well-defined outcome for each two-bit parity check. By inspecting the states written down above, we find that either system is either forced back into the error-free version,
a |000"> + b |111">
or it is forced into the version with a single bit-error,
a |100"> + b |011"> .
In the latter case the parity measurement indicates which bit is in error, so it can be corrected, and the final outcome is always a |000"> + b |111"> = |y>. The same argument can be applied no matter which bit was collapsed in the noisy channel. Therefore as long as the noise only looked at one of the qubits, we always get perfect recovery.