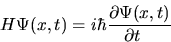
The Schrodinger Equation for the wavefunction of a particle with Hamiltonian H is
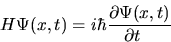
This can be solved by separation of variables. Consider a separable solution:
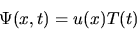
The separated functions satisfy
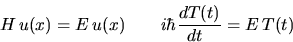
The equation for u is the time-independent Schrodinger equation, and
is also
the eigenvalue equation for H, where E is the
eigenvalue.
It has a set of solutions un(x) with
eigenvalues En.
The equation for T has the solution
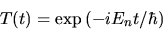
We therefore obtain a set of separated solutions
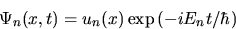
Because of the linearity of the Schrodinger equation any sum of these with
complex constant coefficients is also a solution.
The general solution
of the Time Dependent Schrodinger Equation
(with a Hamiltonian independent
of time) is thus
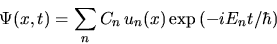
The wavefunction contains our knowledge of the system at time t, and
using the
standard methods of quantum mechanics we can obtain a probability
distribution for
the result of any measurement at any time. For example
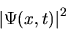
is the probability distribution for the position x of the particle at
time t.
We can then find the mean and standard deviation of this
probability distribution:
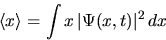
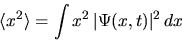
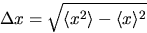
The corresponding results for momentum p are:
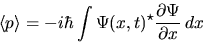
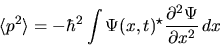
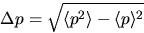
Delta x and Delta p are constrained by the uncertainty principle:
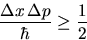
Classical Mechanics predicts a unique x(t), p(t), from precise
initial data x(0), p(0).
In the classical limit of quantum
mechanics we would like to see:
In fact quite a modest superposition of 20 states produces quite a compact
wavefunction, and reduces
the Delta x Delta p product to close to the
uncertainty principle limit.
The Wavepacket Plotter illustrates the time-evolution of
this wavepacket solution in a 1-dimensional box.
The infinite square well is a simple model of a one-dimensional box of width a:
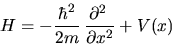
The potential energy function V(x) is given by
V(x)=0 for
0 < x < a and V(x)=infinity for x < 0 and x
> a.
Any quantum mechanics textbook will show that the eigenvalues and eigenfunctions are given by
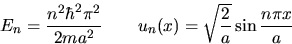
The Wavepacket Plotter generates a wavepacket using eigenfunctions with quantum numbers
centred from nmin to nmax.
THE OLD APPLET HASBEEN REPLAXED BY RGE WAVEFUNCTION PLOTTER. THE TEXT
HERE NEDS UPDATING
The complex constant coefficients
Cn are given by
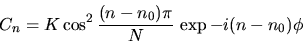
where N = 2dn + 2 and K ensures that the wavefunction is
properly normalised.
(There is no particular reason for this form, except
that it is a `smooth' function of n.)
The phase phi controls where the wavepacket is at t = 0.
The
default value is pi/2, entered in degrees as 90., which produces a packet in the
centre of the box
moving in the positive direction at t = 0.
When the Applet is started it will display the position probability
distribution at t=0.
Check that it looks roughly normalised (height
times width is about one).
Check that the <x> and Delta
x values in the text panel correspond with the plot.
Look at the Cn, Un and
En plots to make sure you understand how the wavepacket
is
made up. The En plot is part of a parabola - you should just
about see the curvature.
Now return to the |Psi(x)|2 plot and note the value of
<p>.
Click on Increment t button, and check that
<x> has increased by about <p>/64
(Remember that
the mass is one, so <p> is effectively the velocity, and the time
increment is 1/64.)
Now click on the Increment t button several times till the wavepacket reaches
the wall of the box.
Notice that <x(t)> increases very slightly,
but at the turn-around it suddenly decreases.
Can you work out why? And
what's happened to the probability distribution?
Now go a bit further forward in time and the wavepacket will go into reverse.
What's happened to <x> and <p> now?
Reset the time to -4.0 and change the plot to <x> vs t.
(This may take a bit of time).
You will now see the wavepacket position and
width compared to the classical limit.
(The classical prediction is based on
<p>=2 exactly.)
Notice that the packet is sharply focussed
around t=0 and is broader at earlier and later times.
Change back to
|Psi(x)|2 and t=8. Notice that the packet fills the
box
and Delta x is close to 1/sqrt(12)=0.289, which corresponds
complete ignorance of its position.
At later times the <x> vs
t plot shows very little oscillation in <x>,
and Delta
x very close to complete ignorance.
So the wavepacket represents a fairly classical particle oscillating in the
box, with our
uncertain knowledge of its initial data leading to an
increasing uncertainty of position at later times.
The spreading of the wavepacket is obvious in classical terms - can you
explain it in
terms of the wavefunction? (Think about how the phase variable
controls the position of the packet.)
Now for a surprise! Look at the wavepacket at t=108. (or whatever is
the current value of n0).
Now how did that happen? Look at
<x> vs t around this region.
In fact the solution is
exactly periodic with period n0. This re-focussing is called a
revival.
Do your ideas about wavepacket spreading explain this? Is the
fact that the revival is exactly
out of phase with the classical motion a
clue?
Now for a bigger surprise. Look at the wavepacket around
t=n0/2 and t=n0/3.
(This may be clearer
with a larger n0 and dn.)
Explore! Explain! Enjoy!
C W P Palmer, University of Oxford.
Wavefunction Plotter © 2017 University of Oxford
Text © 2001 C W P Palmer