Second Year Electromagetism: Problem Set 6

1). * Analyze the case of reflection at the interface between two dielectric surfaces where the incident electric field vector is polarized perpendicular to the plane of incidence. (i.e. the electric field is in the ‘y’ direction as designated in the lectures)

• Obtain the Fresnel equations for E_OR and E_OT.
• Sketch (E_OR/E_OI) and (E_OT/E_OI) as function of q_I for the case when n₂/n₁ = 1.5
• Show there is no equivalent of ‘Brewster’s angle’ in this case.

2). For an electric field polarized in the plane of incidence and for an air-diamond interface (the index of refraction of diamond is 2.42) plot E_OR/E_OI and E_OT/E_OI as a function of the angle of incidence. Find Brewster’s angle and the angle at which the reflected wave’s amplitude is equal to the transmitted wave.

3). An EM wave in the radio band (tens to hundreds of MHz) is normally incident on a highly conductive metal with conductivity s. Find Poynting’s vector within the metal and determine how much power is dissipated in the metal. Do this also for an air-silver interface at optical frequencies w = 4x10¹⁵ rad/s. [silver is nonmagnetic with a conductivity around 6 x 10⁷ (ohm-meters^)-1.]

4). A microwave antenna radiating at 10GHz is to be protected from the environment by a plastic shield of dielectric constant 2.5. What is the minimum thickness of this shielding that will allow perfect transmission (assuming normal incidence)?

5). Prove that it is possible to have a perfectly transmitting pane of material of index of refraction in free space if the thickness of that material is an integer multiple of ½ wavelengths of the EM wave within it. [Rather than crunching through the boundary conditions at normal incidence for a material of a finite thickness, you might find what you have learned from transmission line theory of quite a lot of use here.]

6). An electromagnetic plane-wave is propagating in a plane perpendicular to a dielectric interface and has its electric field polarized in that plane. It approaches the interface at Brewster’s angle. In this case there will be no reflected wave. What is the angle between the incident and transmitted electric field vectors?

7). Write down expressions for linear, Circular, and elliptical polarizations of an EM wave with a given frequency. Sketch the positions of the electric field vectors in each case for illustrative snapshots in time.

8). This problem is off syllabus, but you will encounter it again in 2^nd year optics.
In this case we do not have a homogeneous dielectric, but we are keeping it linear. This means that the equation is now a matrix equation. This is often the case when one is dealing with crystalline solids. What would happen if an EM wave in free space encounters a crystal at an angle with the following dielectric property:

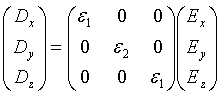
The interface between the crystal and free space forms the x-y plane. An EM wave approaches the crystal face in a plane normal to that face, but at an angle q with respect to that normal. Calculate or reason what would happen for the two cases of an EM wave plane with the electric field vector polarized in the plane of incidence and a wave polarized perpendicular to the plane of incidence. [These crystals do exist and are called ‘birefringent’.]

9). I do not think this is an off Syllabus Question, but it does require thought:

Assume that the index of refraction in a dielectric medium is different for right and left circularly polarized light of a given angular frequency. The index of refraction takes the form:

Where n and b are real and the plus and minus signs refer to right and left circularly polarized plane waves respectively.

Write a linearly polarized plane wave as a linear sum of left and right circular components. (You need to invent a new basis to do this…just like you did in linear algebra…there is the , basis you are familiar with …but equally we could have a different bases with ‘left’ and ‘right’ orthogonal basis vectors. Of course, the ‘left’ and ‘right’ components have the advantage of each propagating with their own obvious speed.)

Show that in this medium an initially linearly polarized propagating plane wave has it’s plane of polarization rotated as it propagates through this medium.

Find the angle through which the plane of polarization is rotated as a function of the distance z into the medium. [4018]

* - This problem is long but should not be difficult.