Second Year Electromagetism: Problem Set 4

1). A pair of conductors with a capacitance per unit length C and inductance per unit length L. Reproduce the calculations in lecture to generate equations showing that the voltage and current as a function of position and time follow wave equations. What is the significance of the characteristic impedance? Why is the characteristic impedance independent of frequency? Explain the approximations that make this possible and where they might break down.

2). A long length of transmission line of characteristic impedance Z₀ is terminated by a resistor of resistance R and a further length of line of length L₀ (a stub) and characteristic impedence Z₁. (See illustration below)

Find the impedance of the resistor-stub combination and show that, depending on the length of the stub the load can be inductive or capacitive.

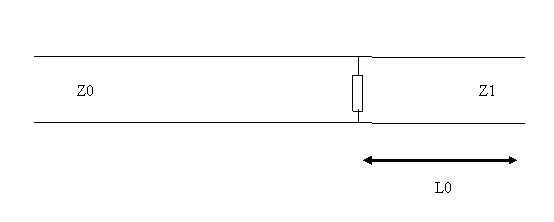
3). A 75 ohm coaxial cable is split into two coaxial cables of the same characteristic impedance (also 75 ohms). Show that the incoming signal will not just simply split into two and send ½ the power down each line and that, indeed, there will be a reflection. Find the value of the reflected and transmitted average power down each line.

4). Construct a splitting device for the situation in the problem above where the transmitted power is evenly split and there is no power reflected back toward the source. [There are at least two ways I know of to do this, one of them is completely symmetric meaning that it will work no matter which terminal of the device is connected to which cable…either transmitting or receiving.]

5). A signal is sent down a 300 ohm conductor pair. At the end of this line is a 100 ohm resistive load with a tuner that presents 10nH of inductance. Design a stub that will cancel the reactive load and prevent reflections back down the line if a 100MHz signal is sent down the line.

6). Show that, by introducing a ¼ wave section of characteristic impedance Z2 between two transmission lines of impedances Z0 and Z1 that all the power coming down the Z0 line will be transmitted if Z2 is properly chosen and find that value in terms of Z0 and Z1.