Second Year Electromagetism: Problem Set 3

These questions can be studied at the end of term.

1). Write down Maxwell’s equations for electromagnetic fields in vacuo. Show how each law comes from the integral laws of electromagnetism.

Show that the conservation of electric charge requires the addition of the displacement current in the unmodified (pre Maxwell) Ampere’s Law,

.

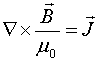2). Starting from Maxwell’s equations show that the electric field and the magnetic fields independently satisfy a wave equation of motion in space and time in free space with no charges present.

3). Starting from Maxwell’s equations, derive explicit expressions for the electric and magnetic fields of an electromagnetic wave of angular frequency w propagating in free space in the z direction and whose electric field vector is of magnitude E₀ lies in the x direction. Sketch in 3-dimensions the electric and magnetic fields at one moment of time over a distance of some two wavelengths. Find the phase and group velocities of the wave.

4). Now that we are looking at time dependent electric fields explain, using Maxwell’s equations, why it is no longer possible to express E as the pure gradient of a scalar function but it is still perfectly OK to continue to express B as the curl of a vector function (A). A hint on how to explain this is related to the fact that no magnetic charges seem to exist, and this experimental fact is built into Maxwell’s equations as they are taught.

It would be nice to recover somewhat from this situation and find a way to represent E in terms of potentials again.

· In the equation substitute the expression for the vector potential A in for B and recognize that we now have the curl on both sides of the equation. Can we then just identify E with one side? Why or why not?

· Use this to derive a new time-dependent expression involving V and A to obtain the electric field vector E.

· In the absence of currents and free charges, find the equations of motion that V and A will obey given Maxwell’s equations.

5). Suppose we are given the following electric and magnetic fields:

; .

Show that these fields satisfy all of Maxwell’s equations and determine the charge density r and the current density J. Describe the physical situation that gives rise to these fields. (The function Q is defined to be zero when the argument in parentheses is negative and one when the argument is positive.)

6).! A 3MHz plane wave in free space has a peak electric field of 0.1V/m. Calculate the peak open circuit voltage generated in a ten turn receiving loop aerial whose area is 1m² and which is oriented so that its plane contains both the electric vector and the direction of propagation. What happens if the loop (of negligible resistance) is short circuited? (Might be a good idea to give the loop a resistance R and calculate the extremes in both cases. And do not forget that a loop of wire does have a small self-inductance L.)

7). Consider electromagnetic waves in free space of the form

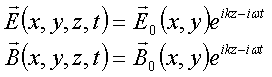
where E₀ and B₀ are in the xy plane (but are not necessarily plane wave constant vector fields).

· Derive the relation between k and w as well as the relation between E₀ and B₀. Show that B₀ and E₀ satisfy the equations for magnetostatics and electrostatics in free space. What is the relationship between k and w in terms of e₀ and m₀?

· List or re-derive the boundary conditions for E and B on the surface of a perfect conductor.

· Consider a wave of the above type propagating along the long axis between a pair of perfect cylindrical conductors which have a common axis in the z direction. There is a vacuum between the two cylinders. The inner conductor as a smaller radius a compared to the outer cylinder of radius b (but not so small as to be negligible). Sketch the electromagnetic field pattern for a particular cross section. Indicate the signs of the charges and the directions of the currents in the conductors. At the end of the conductors a resistance of 377 ohms connects the inner and outer conductors.

· Derive expressions for E and B in terms of the charge per unit length l and the current I in the central conductor. [4003]

8). The configuration of conductors in the previous problem you have seen before. Calculate the inductance per unit length L and the capacitance per unit length C for this system in terms of physical constants and the dimensions of the conductors. Find the quantity and comment on the value you get for this given the results of the previous problem.

9). The wave of question 3 approaches normally from negative z a perfectly conducting metallic mirror surface lying in the plane z = 0. No energy is absorbed and a reflected wave of the same amplitude propagates in the reverse direction. Being a perfect conductor, the boundary condition determining the reflected wave is that the component of electric field parallel to the surface is zero at all times.

Find expressions for the electric and magnetic fields of the reflected wave as a function of z and t. Adding together the incident and reflected waves, deduce expressions for the total electric and magnetic fields of the combined wave. Find the group velocity of the combined wave. Find the amplitude of the total electric and magnetic fields at the metallic surface.

10).* For Problem 7 find the direction and strength of Poynting’s vector. Explain it’s meaning.

· The momentum density of an electromagnetic wave is given by where S is Poynting’s vector. Find the direction and magnitude of the average momentum crossing a plane parallel to the xy plane that cuts the conductors of problem 10.

· Suppose that w = 0, meaning that we no longer have the time dependent case. What is the direction and magnitude of the momentum now? This is particularly interesting because we can imagine connecting a battery to one side of the two cylinders and a resistor to the other side. It is clear that energy is being transported between the two conductors and being dissipated in the resistor yet the entire system is at rest.

· If momentum is flowing from the battery to the resistor through the Electric and Magnetic fields, how can we square this with the conservation of momentum?

· Given that EM fields have a momentum density it is likely they have an angular momentum density as well. Use your knowledge of classical physics to write down a likely expression for the angular momentum density carried by electric and magnetic fields.

11). A parallel plate capacitor has circular plates of radius a separated by an air space of thickness d (d<<a). During a certain time interval, the capacitor is charged by a constant current I flowing in the circuit to which the capacitor is connected. Obtain expressions for the rate of increase of energy stored in the capacitor.

· From the voltage across the capacitor and the current

· By considering the energy stored in the volume between the plates

· By integration of the Poynting vector over a suitable surface.

Show that the expressions you have obtained are compatible with each other. [You can assume that the fields on the edge of the capacitor can be neglected.]

! - These problems are somewhat more challenging.

* - These problems are mostly off the syllabus.