Second Year Electromagetism: Supplemental Problems for Michaelmas Term

 

Upon speaking to several colleagues they all preferred smaller tutorial problem sets and then an extensive list of ‘supplemental problems’. I have made an effort to do this. These are the supplemental problems for MT.

 

Note to Students: During the course of your studies I would highly recommend that you, at some point, attempt these problems. These problems are often challenging, so be warned!

 

1).* Go back to Problem 3 in Problem Set 1 and try to calculate the potential using the multipole expansion out to and including the quadrapole term. Does this expansion even contain a dipole term? If instead of a line of charge extending from +a/2 to –a/2 we did this same calculation for a line of charge from the origin to +a would there be a dipole term then? Explain what is going on. (Thinking about the multipole expansion of a point charge that is not located at the origin might help.)

 

2). Example 3.4 in Griffiths goes through a calculation of the potential inside a semi-infinite pipe of rectangular cross section. Calculate the potential inside a metal cube of sides b where the origin forms one of the vertices of the cube. All sides are held at zero potential apart from the top face (the face represented by the z=b plane) which is held at a potential V0. Use separation of variables and solve Laplace’s equation for the potential everywhere inside the box.

 

3).!! Problem 2.49 on page 108 of “Introduction to Electodynamics” by D. Griffiths. This is a good problem for the break between MT and HT.

 

4). A sphere of radius b has uniform charge density p within its volume except for a small spherical hollow of radius a located a distance c from the centre. [1022]

  • Find the potential at the centre of the hollow sphere.
  • Find the electric field at that same point.

 

5). A magnetic dipole of strength m is placed in a uniform constant magnetic field B0 with the dipole moment directed opposite to the field. Show that in the combined field, there is a certain spherical surface, centred on the dipole, through which no field lines pass.  We know from popular accounts in the scientific magazines we all read (Discover, New Scientist, Scientific American, and heck…maybe even Omni) that magnetic field lines cannot enter a superconductor. Explain how this problem can relate to that one.

 

6). A ‘Type 1’ superconducting sphere is placed in a uniform constant magnetic field. Such superconductors expel all magnetic fields such that B = 0, and H = -M (the relative magnetic permeability mr = 0 as well).

  • Given that no magnetic field is permitted within a superconductor and that currents can flow freely without dissipation on its surface, use the magnetic field equations to obtain boundary conditions for the magnetic fields just outside a superconductor.
  • Using the concept of the magnetic scalar potential and the boundary conditions just found, find the magnetic field everywhere outside the superconducting sphere.
  • Calculate the surface current on the sphere.

 

7).  Show that the solid angle subtended by a circular loop of radius a at a distance b along its axis of symmetry is given by:

.

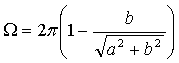Hence show that the magnitude of the magnetic induction at this point of such a loop carrying current I is given by 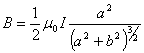. Compare this result with that obtained by direct application of the Biot-Savart rule. Perform the closed loop path integration through the centre of this loop and confirm that it gives the result expected from Ampere’s Law. (The easiest path to use is one that goes through the centre of the loop from a large negative distance R to a large positive distance R and then closes the loop with a half-circle at large constant R. Then let R tend to infinity.)

 

8). A straight conducting wire of circular cross section has resistance R and carries a current I. Find the value of Poynting’s vector at the surface of the wire in terms of its radius a and show that the total power crossing the surface of the wire per unit length is I2R. Is the energy entering or leaving the wire?

 

Show that the energy is dissipated uniformly throughout its volume (one way to do this is through the divergence of Poynting’s vector within the wire). Note that throughout this problem we are assuming this ‘wire’ has the same permittivity as free space. This problem will be rectified later in the course when we consider now matter responds to electric fields.

 

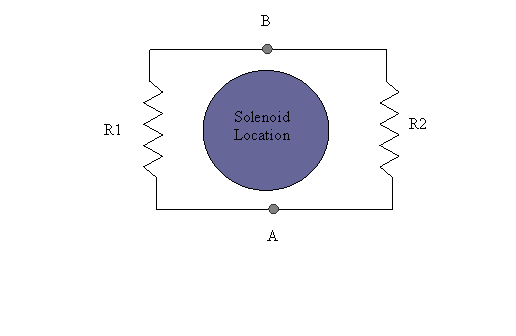
9).! A long solenoid runs perpendicular to the page in the figure below. The current through that solenoid is varied so that the magnetic flux through the circuit varies linearly with time (where a is a constant). Two voltmeters are connected between points B and A as shown. The voltmeters are ideal (meaning they draw no current themselves and can measure  between the two points without effecting that potential) and they are both connected with their positive sense at point B. Give expressions for the readings on the two voltmeters and be careful of the relative signs. Explain how it is possible to obtain two different readings when the meters are connected to the same points on the circuit (an apparent violation of Kirchoff’s voltage law)!

 

 

10).! Imagine a very long solenoid with radius R, n turns per unit length, and current I0. After waiting a long time the current I0 is slowly reduced to zero at a constant rate a. Calculate the resulting electric fields that would appear inside and outside the solenoid while this is happening. Sketch them and their directions.

  • Coaxial with the solenoid are two hoops. One of radius a<R and the other with radius b>R. The inner hoop has a total charge +Q around its rim and it is permitted to spin about the central axis. The outer hoop has a total charge –Q and is also permitted to spin about the same axis. This is also an axis parallel with the magnetic field.  Assuming the two hoops each have a mass m0 and are at rest before the current is reduced, describe as quantitatively as you can what happens as the current is reduced and which direction the hoops are spinning (if at all) when the current falls to zero.
  • Is angular momentum conserved in this problem?

 

11).  The electric field of an electromagnetic wave in vacuum is given by

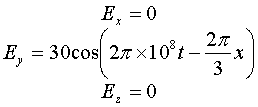
where E is in volts/meter, t in seconds, and x is in meters. Determine

·        The frequency f,

·        The wavelength l,

·        The direction of propagation of the wave,

·        The direction and strength of the magnetic field. [4001]

 

12).!  Question 10 of this problem set might have set off alarm bells if the Oxford term were not so intense. Here is a problem where the system was entirely at rest, but when the current of the solenoid was decreased to zero the hoops were spinning! Is angular momentum conserved or not? Use the formula above to estimate that rate of spin assuming a given mass m0 for the two hoops.

 

! – These problems are more challenging.

* – These problems are mostly off syllabus.