Shannon Game
This concerns the Shannon switching game on nodes. This should not be confused with the Shannon switching game on edges, which is much simpler and consequently less interesting. A fascinating and fun example of the Shannon game on nodes is the board game Hex.
These pictures show two rather elegant examples of weak links in the Shannon game. The red nodes are terminals:
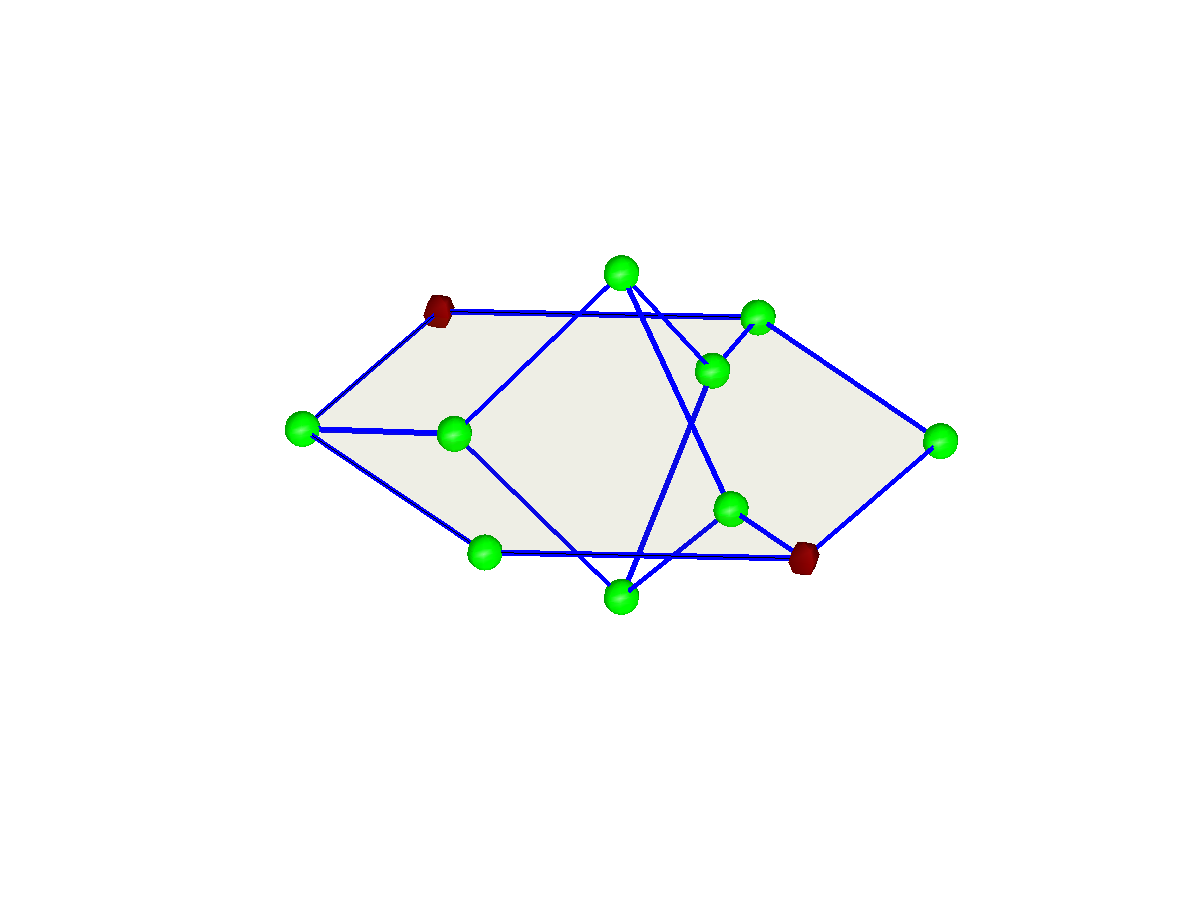
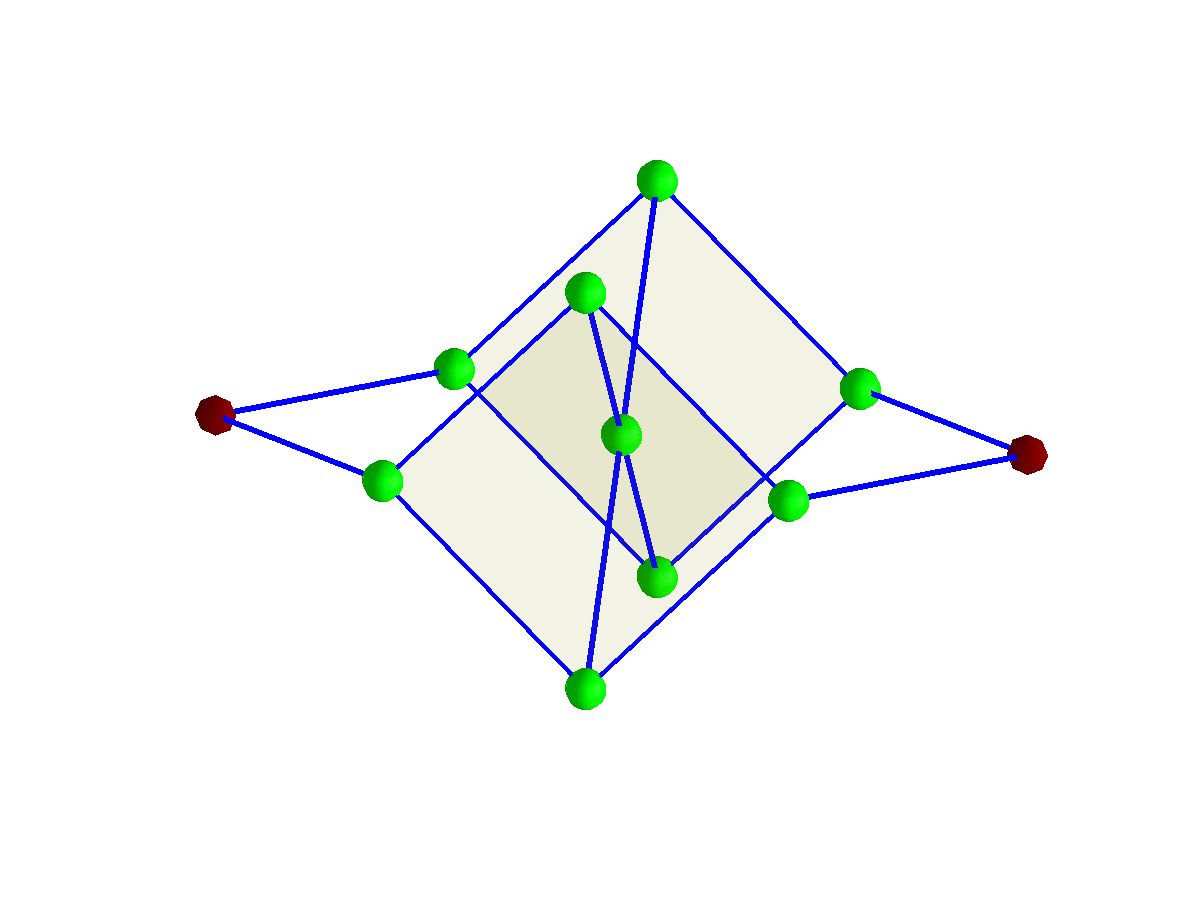
The first case has a 3-fold rotation symmetry so one can assign the terminals in multiple ways: not only the three ways obtained from the symmetry, but also a further three obtained by colouring the degree-3 terminal green and colouring its degree-3 neighbour red. The second case is unusual in having many pivots (winning opening moves for Short). It is the only minimal weak link of weight 9 that has 5 pivots. The only losing opening moves for Short are the four neighbours of the central node.